こんいちは、加茂駅前校の津村です。
今回は前回の続きからです。（↓前回の内容はコチラ！）
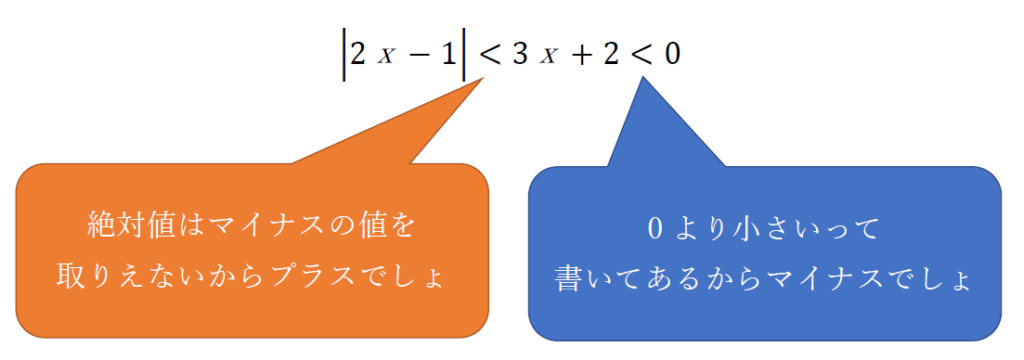
前回、とある高校生が『納得できない』としていた問題。本人の思考をコメント付きで考えるとこういうことになります。
確かに、絶対値というのは＋,－がその値である事を示すものなので、｜ⅹ｜＝3であればｘ＝±3 になりますし、｜ⅹ｜≦3とであれば －3≦ｘ≦3 となります。
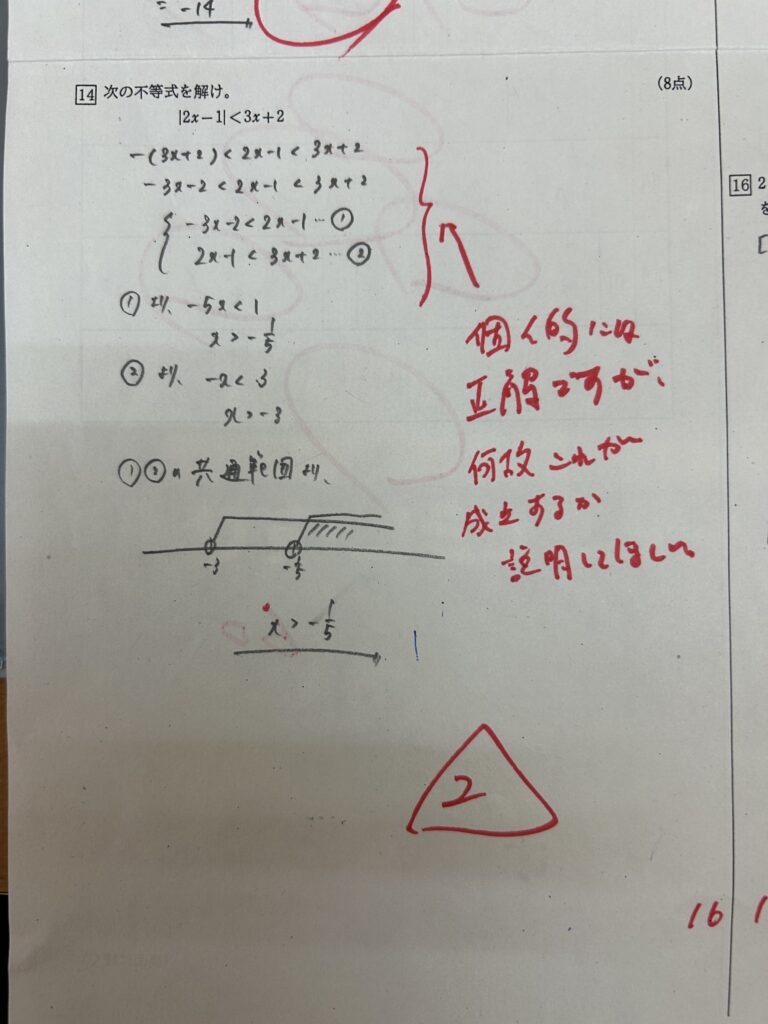
そのあとの式の整理も数直線上に図示した整理もミスはなく実際の答え(模範解答)を見ても答えはｘ＝－1/5 となります。
さらに言えば、この回答を他の高校の数学の先生に見せた場合、『ウチなら〇にしてた』という反応を返されても不思議ではありません。
では、何がまずかったのでしょうか？
それは絶対値の側より大きくなるはずの3ｘ+2が『本当に正の値なのかどうか』が説明されていないことにあります。
要は、｜ⅹ｜＝－5 なんてものはあり得ないですし、｜ⅹ｜≦－5 なんて値も取りようがありません。
つまり絶対値より大きな値を取るはずの3ｘ+2が負の値になるというのは矛盾が生じるので、そういった値は排除しなければならないのです。
では、この矛盾点を出さないように3ｘ+2＞0という式を導入して解いたものがコチラになります。
はい、先ほども述べた通り、答えは結局ｘ＝－1/5 となります。
『じゃあ、結局意味がない事の説明を求められてるなら理不尽な採点じゃないの？』となるかもしれません。しかし、この子が通う学校は合格実績の中に旧帝大レベルの学校が出るほどの進学校となっています。特に京都大学レベルにまでなってくると、『解答の最後の一押しが公式・定理の理屈に合うのかどうかを考えさせる』といった、難解なひっかけ問答も存在しているのもまた事実です。とはいえ、志望校によって学校内の生徒の〇×を変えるわけにはいかないので、この採点は『適正な判断による採点である』と言えるわけです。
↑そのうえでコメントからも×にするのは心苦しいといった様子が見て取れます。うん、気持ち分かるよ！
このように、いろいろな採点に関しては各先生の思惑や価値観があり、完全に統一するのは難しいものです。その価値観の違いを比べる事で『何をしてほしいのか』を考えると、学校内の事情など思いがけない発見があるかもしれません。
みなさんも謎な採点があった場合、ぜひいろいろと考えてみてください。
【CM】
いよいよ今週末！リンクス個別指導加茂駅前校では、現在泉川中学校生を対象とした『定期テスト対策攻略講座』の参加者を募集を行っています。
友人からの紹介があった場合は完全無料で対応させていただきます！
この機会にぜひリンクス個別指導をご利用ください。