こんにちは、加茂駅前校の津村です。
本日はこちらの解答編です。
さて、では改めて問題を見てみましょう。
反比例のグラフ
そもそも右上のグラフを通っている点Aの座標に関して何も言っていない(場所が決まっていない)ので、グラフの式が出せるとは言え、一見手掛かりがないように思います。(ちなみにグラフは反比例の式に点(4,-8)を代入して比例定数-32ということが分かります。中学2・3年生の皆さんは出来ましたか?)
しかし、ここで三角形の底辺と高さの関係を思い出してみましょう。
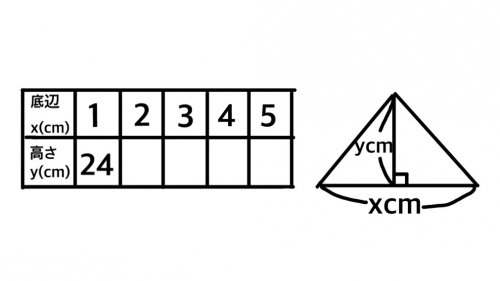
そう、この2つは反比例の関係。つまり、どういう組み合わせで掛け算を行っても一定の値を取ることが分かります。
つまり、点Aの場所がどのような位置であろうと、AB×BOの掛け算の値は同じ。つまり32となります。
あとは三角形の面積なのでAB×BO÷2を計算すればよいので答えは16となります。
さて、では本題。新傾向としてこの問題をピックアップしましたが、『この問題の新傾向的な観点はどこにあるのか?』をお話ししましょう。
前回のブログにてお話ししたこの内容。
『昨年度、大学入試で実際に出題された読解力・学習したことを活かすような問題が、今後高校入試へと降りてくることが予想される。』
今回、皆様に出題した問題はこの内容がまざまざと表現された良問でした。(ちなみに、この問題は学校準拠テキストの類題として拝借したものです。)
『面積の等しい三角形の底辺と高さの関係が反比例する。』という内容は、小学6年生の算数でひっかけ問題の定番(×をしたときの関係が面積の値とズレるので)として、非常によく見かけます。また、文章を読み取って反比例の関係かどうかを見分けるといった問題で三角形の面積についてが出てくるのは小6でも中1でも頻繁に出題されます。
そんな、『面積の等しい三角形の底辺と高さの関係が反比例する。』という関係を、座標の上でもすぐに思い出し活用できるのかが非常に重要になってくるという、まさに学習したことを活かす問題です。
ここからは、こういった学んだことを活かすための授業もどんどん活発となってきます。知識を蓄積することももちろん大事ですが、活用する練習が必要である以上、知識の習得はスピーディーである必要があります。
どういった状況でもしっかりと成績を残せるようリンクス加茂駅前校は努めていきますので、興味のある方は是非お立ち寄りください。




