こんにちは、加茂駅前校の津村です。
本来、塾のHPブログなので、政治的に議論が起こりやすいネタは扱うべきではない(炎上したくないし……)と考えているのですが、今回は加茂に関わる内容だったの、取り上げてみたいと思います。
事の発端は、1/19に掲載された読売新聞のこの記事でした。
https://www.yomiuri.co.jp/expo2025/20240119-OYO1T50010/
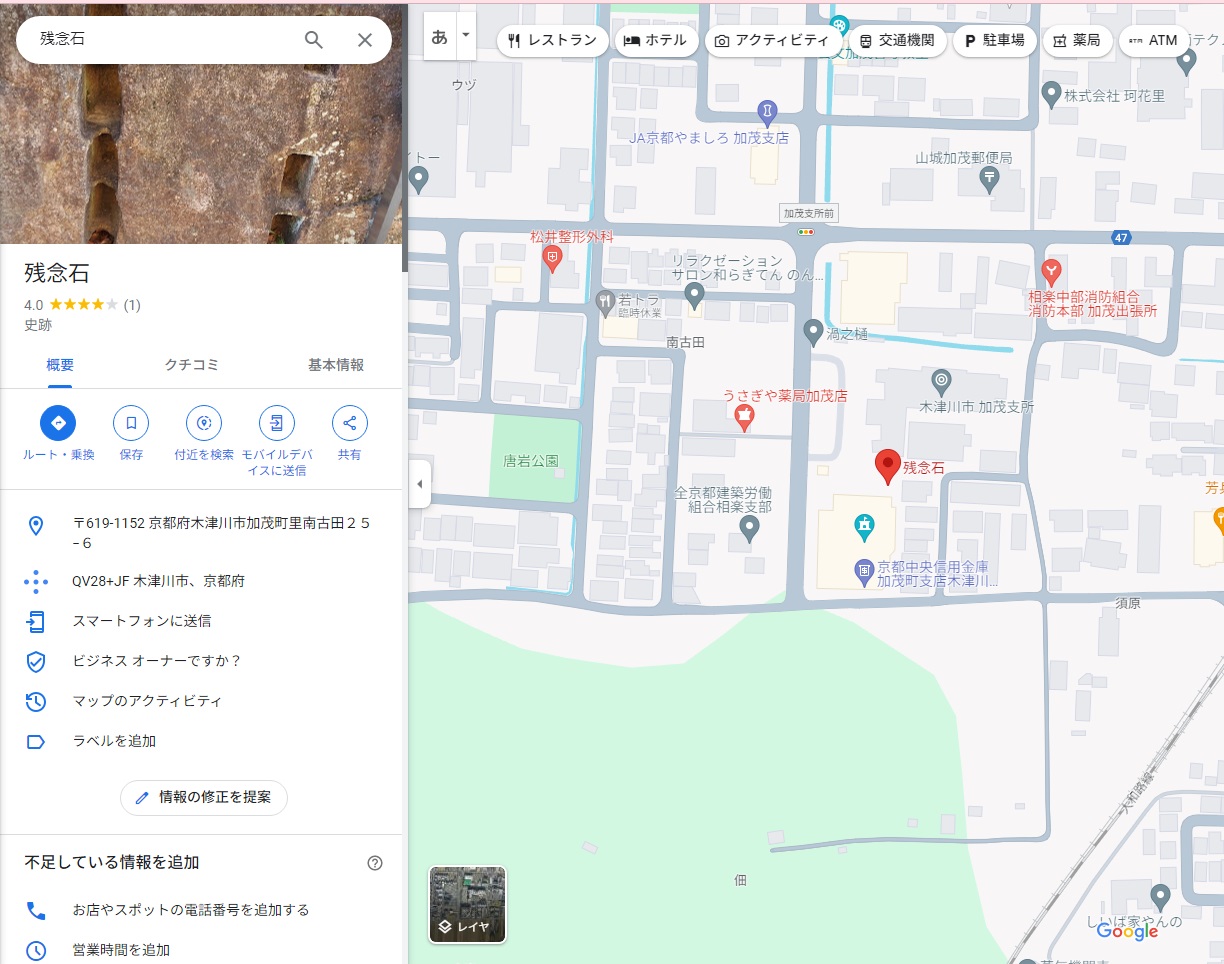
この記事を端的にまとめると、旧加茂町の西側にある『赤田川』の流域にある『残念石』を万博会場の建材に利用する計画が上がっているという記事でした。

(記事内より写真を引用)
残念石は江戸幕府2代将軍の徳川秀忠が大坂城の再建工事を行った際に、当時の加茂界隈の大名であった藤堂高虎(戦国時代の築城名手。主家を変えまくった事でも有名。)の指示によって切り出されたものの、結局使われなかった石垣用の巨石です。
この残念石を大阪万博の会場のトイレ・休憩所の支柱として利用して、海外の人々に当時の石材加工技術を見てもらおうというプロジェクトとの事です。
この残念石のリノベーション報道に対して、X(旧Twitter)の反応は
・文化財をトイレの柱に使うという発想が気持ち悪い! ・賛成者は古墳や石仏もリノベーションするのか! ・歴史的価値もわからん奴の頭の方が『残念』だろ!
と、まあこのように大炎上してしまっている訳です(汗) 感情むき出しで怖いなぁ
確かに、歴史的価値の高いものを持って行ってしまうという事は、歴史の保存という観点から見れば『冒涜的』ともとれるのは確かです。しかし、残念石を始めとした加茂の史跡の保存・広報をしているNPOもこのプロジェクトを支援しているため、もしかすると今回の報道の中身だけでは語られていない事案があるようにも感じます。
そもそも、炎上している状況においての批判的意見というのは、だいたい感情に任せた物が多いので、少し落ち着いていろいろと調べてみることにしました。
残念石の制作と発見
当時の加茂エリアは藤堂高虎の命令で1000個ほどの巨石が赤田川南西の大野山より切り出され、木津川の水運を利用して大阪城まで運搬されました。切り出された巨石のうち600個ほどは実際に大阪城の再建に利用されていましたが、城というのは軍事施設なので、いつ戦いで壊されるかもわかりませんし、それでなくても日本は大地震の多い国なので、壊れてから切り出していては再建が遅々として進まないという問題がありました。
残念石は、いざ城壁が壊れた際のスペアとして保存されていました。(余談ですが、豊臣政権下の伏見城は完成直後に慶弔伏見地震で倒壊するというショッキングな出来事もありました。当時の高虎は豊臣家臣だったので、城壁のスペアを準備するという思考は自然なものだったと思います。)
しかし、その後太平の世となり大きな災害に見舞われることおなかったため、切り出した巨石の事は完全に忘れ去られていきました。

残念石が発見されたのは1975年。赤田川流域の護岸工事を行った際に、誰かが加工した形跡のある大きな石が60個ほど発見され、当時の文献と照らし合わせることで上記の内容が明らかとなったのです。
歴史資料としての保存
そんな残念石の保存ですが、その場所をそのまま史跡として指定して保存したのかと言われると全くそんなことはありません(笑)
例えば、木津川市加茂支所(下の写真)にはここから発掘された残念石の1つを持ってきて展示しています。他にも切り出し作業当時に高虎が滞在したとされる常念寺の境内にも移設されたものが残っています。
また、残念石は加茂だけでなく大阪城の内部や周辺にも存在しています(下の写真)。石切り出しは加茂以外にも小豆島や六甲山地でも行われており、同様にして発見されています。そのうち、小豆島から発見されたものは大阪城天守閣前に持ってこられたものも存在しています。
これらの例から、そもそも保存目的であちこちに移設・移譲が行われている以上は残念石を移動させてはいけないという理由はないということになります。
また、歴史資料の保存というのは、何も『その場に残すこと』だけではありません。実際にこの地でどんな歴史があったのかを伝えること、この地にそのような歴史があることを知ってもらうという事も大切な歴史資料の保存につながっています。(まあ、知らなかったらそもそも保存しようという発想になりませんので……)
そこで、ここ数日の間、実際に僕が授業を受け持った子供たち数名に今回の件を話してみたところ、残念石の存在を認知していた子供たちは6~7割にのぼっており、加茂エリアにおいて残念石についての周知活動そのものをしっかりと行っている様子が見て取れました。
ただ、今回の一件以前についての残念石の世間一般の認知度については、決して高いとは言えない状態でした。実際にGoogleを使って過去の記事を検索すると、内容としては『関西のスポーツ紙のコラム』『辺境歩きを趣味とした方のブログ』『歴史マニアの遺跡探訪ブログ』といった趣のものがほとんどでした。
以上から、加茂の残念石は『地元民からはそこそこの認知度ではあるが、世間一般からすればマニアがたまに着目する程度の認知度』という状況だったことが推察されます。
邪魔だった残念石?どうせ動かすんだったら……
さて、今回の一件に話を戻します。
今回いろいろと調査を進める中で、残念石の万博会場での活用に至った背景となるであろう情報も入手できたので、この件についても記載しておきましょう。
この資料は京都府と木津川市が委託している加茂西側の道路のバイパス整備の資料です。この工事は道路周辺の渋滞解消・視界確保と歩行者・自転車の安全確保のために計画されている工事です。この付け替え工事のコース上に残念石が発見された場所があるのです。
そういった背景から、実は2022年の初めごろから出土していた残念石をほかの場所に移設する申請を木津川市は京都府・国に打診しており、その作業にを進めていく方針だったという事です。
https://www.kyoto-np.co.jp/articles/-/718320
(参考:京都新聞 2022年1月25日発行記事より)
この流れがあれば『残念石を万博会場へ!』という流れも納得はできます。
地元への周知はある程度行えていた残念石も、他地域のような観光地化された史跡に比べると非常に地味で、歴史マニア・秘境マニアがたまに着目する程度の認知度であるのであれば、いっそ世界中からの客が見込める万博会場に残念石を寄贈することで、加茂に対しての興味を持ってもらうきっかけとなるように移設を容認することも何ら不自然な思考ではありません。
残念石から考えるニュースの見方
最後に、今回のニュースについての個人的な見解を書き記します。
残念石の利用についての意見は『あまりいい気がしない』というのが正直なところです。実際に加茂で働くことで土地勘があり、歴史的な価値というものに対してのアンテナが張っているタイプの人間である以上、あるがままの姿で残念石の事を知ってもらえることがベストだと考えます。しかしながら、先述の通り一部のマニアックな人にしか知られることのなかった現状から、多くの人に知ってもらいたいという思いがあるならば、それは応援したいとも思います。
以上から、僕個人の意見としては『心情的にはNGだが、協議のうえでの決定であれば応援したい。』いった形になります。
大阪万博2025は建設計画の詰めの甘さ・現段階での国民の興味関心の低さに加え、東京オリンピックの誘致活動の際に裏金が動いていたという報道から、昨今の国家事業についてはどうしても批判的な意見を向けられがちな傾向にあります。そんな中で歴史的に貴重なものをリノベーションするという形での報道は反対意見を持つ人々からは格好の批判ネタとなりました。しかし、批判的意見を向けていたほとんどの人が、『罰当たり!』『発想が陳腐!』というような言説であり、先ほどのように残念石の保存についての知見や現状について、調べて理解したうえでの批判を行っているとは、どうにも思えないような投稿が散見されていました。どちらかというと『万博反対!』『箱モノ事業で儲ける悪徳政治家を許すな!』という論調に引っ張られた投稿が多いように見られました。
様々なニュースにおいて、報道は『情報の取捨選択』が行われたものが提示されます。今回の例であれば『残念石の移設は割と頻繁に行われている』『バイパス工事の関係で元あった場所からはすでに移動済みである』といった背景情報を知っているか否かで受け取り方が大きく変わってくるニュースであると思います。
日々報道されるニュースに対して背景情報も含めた思考判断をしていく姿勢を持ち、通ってくれている子供たちが正しく判断できるような情報提供ができるように過ごしていこうと改めて思わせる騒動となりました。